2015丹东一模理科数学试题及答案(8)
学习频道 来源: 丹东一模 2025-02-26 大 中 小
(20)(本小题满分12分)
解:(I)根据已知,椭圆的左右焦点为分别是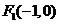 ,
,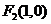 ,
,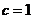 ,
,
∵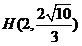 在椭圆上,
在椭圆上,
∴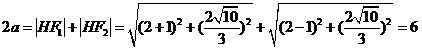 ,
,
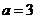 ,
,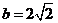 ,
,
椭圆的方程是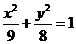 ; …………(6分)
; …………(6分)
(II)方法1:设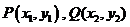 ,则
,则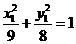 ,
,
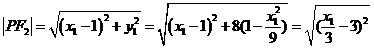 ,
,
∵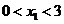 ,∴
,∴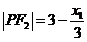 ,
,
在圆中,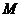 是切点,
是切点,
∴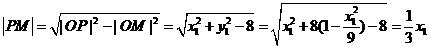 ,
,
∴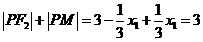 ,
,
同理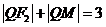 ,∴
,∴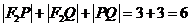 ,
,
因此△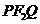 的周长是定值
的周长是定值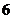 . …………(12分)
. …………(12分)
方法2:设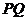 的方程为
的方程为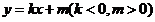 ,
,
由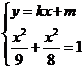 ,得
,得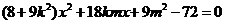
设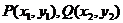 ,则
,则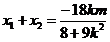 ,
,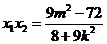 ,
,
∴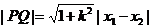
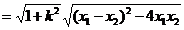
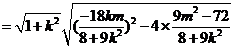
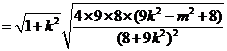 ,
,
∵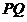 与圆
与圆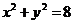 相切,∴
相切,∴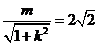 ,即
,即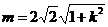 ,
,
∴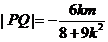 ,
,
∵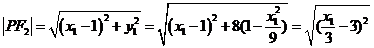 ,
,
∵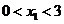 ,∴
,∴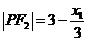 ,同理
,同理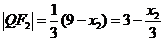 ,
,
∴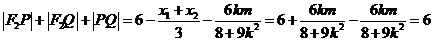 ,
,
因此△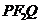 的周长是定值
的周长是定值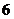 . …………(12分)
. …………(12分)
(21)(本小题满分12分)
解:(I)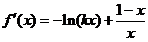 ,由题意
,由题意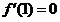 ,得
,得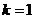 , …………(2分)
, …………(2分)
此时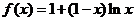 ,定义域是
,定义域是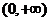 ,
,
令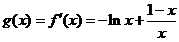 ,
,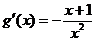
∵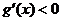 ,∴
,∴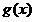 在
在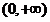 是减函数,且
是减函数,且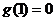 ,
,
因此当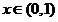 时,
时,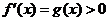 ,当
,当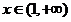 时,
时,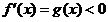 ,
,
∴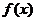 在
在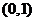 上是增函数,在
上是增函数,在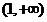 上是减函数; …………(6分)
上是减函数; …………(6分)
(II)不等式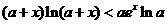 可以化为
可以化为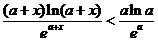 ,
,
设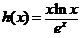 ,则
,则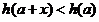 ,
,
即判断是否存在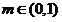 ,使
,使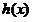 在
在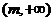 是减函数, …………(8分)
是减函数, …………(8分)
∵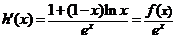 ,
,
∵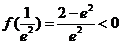 ,
,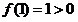 ,
,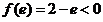 ,
,
∴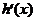 在
在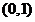 和
和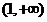 上各有一个零点,分别设为
上各有一个零点,分别设为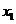 和
和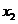 ,列表:
,列表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
极小 |
|
极大 |
|
∴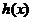 在
在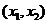 是增函数,在
是增函数,在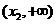 是减函数,
是减函数,
∵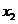
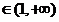 ,∴不存在这样的
,∴不存在这样的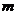 值. …………(12分)
值. …………(12分)
【注意】“当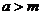 时,不等式
时,不等式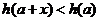 对任意正实数
对任意正实数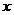 都成立”这句话符合必修1中函数单调性定义,说明
都成立”这句话符合必修1中函数单调性定义,说明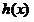 在
在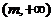 是减函数.
是减函数.
 (23)(本小题满分10分)选修4-4:坐标系与参数方程[来源:学。科。网]
(23)(本小题满分10分)选修4-4:坐标系与参数方程[来源:学。科。网]
解:(I)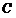 的极坐标方程化为
的极坐标方程化为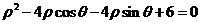 ,
,
∴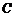 的直角坐标方程
的直角坐标方程 是
是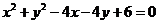 ,
,
即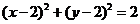 ,
,
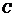 的参数方程是
的参数方程是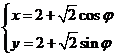 ,
,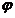 是参数; …………(5分)
是参数; …………(5分)
(II)由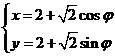 (
(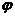 是参数)得到
是参数)得到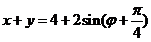
∴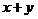 的最大值是6,最小值是2. …………(10分)
的最大值是6,最小值是2. …………(10分)
(24)(本小题满分10分)选修4-5:不等式选讲
解:(I)当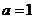 时,此不等式为
时,此不等式为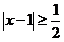 ,解得
,解得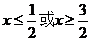 ,
,
∴不等式的解集为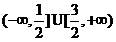 ; …………(5分)
; …………(5分)
(II)∵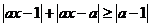 ,
,
∴原不等式解集为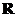 等价于
等价于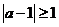 ,∵
,∵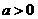 ,∴
,∴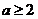 ,
,
∴实数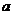 的取值范围为
的取值范围为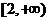 . …………(10分)
. …………(10分)
学习关键字:
学习频道 | 高中生综合素质评价 | 北京开元网站登录入口 | 上海开元网站登录入口 | 天津开元网站登录入口 | 学习地图 | 重庆开元网站登录入口 | 贵州开元网站登录入口 | 广西开元网站登录入口 | 吉林开元网站登录入口 | 开元网站登录入口排名 | 高考成绩查询 | 高考录取查询 | 高考志愿填报 | 教务管理系统 | 高考专题 | 开元网站登录入口手机版 | 学习频道手机版